In my experience, saying “quantum field theory” is a very effective way to lose your audience. The merest mention of higher dimensions causes eyes to glaze over, and even the most intelligent listeners will often assume that the ideas will be too complex for them to follow, and tune out. To be fair, quantum field theory, or QFT, can involve rather advanced math and abstract concepts. However, I believe that a conceptual understanding of QFT is not only attainable, but interesting and useful for understanding how the world works.

Before I continue, allow me to issue a disclaimer. I am not a physicist. I am not qualified to talk about quantum field theory in any significant detail. I do not claim to have a perfect understanding of this rather complex theory, nor do I claim to be able to impart such an understanding. What I have done is pieced together a mental model of the basic concepts of quantum field theory, which I have found interesting to think about and rather useful in the past. This model has helped me understand various concepts in biology, chemistry, and physics, and I believe it has allowed me to understand the world around me a bit better. As such, I wish to share this interesting and useful little tidbit I’ve found.

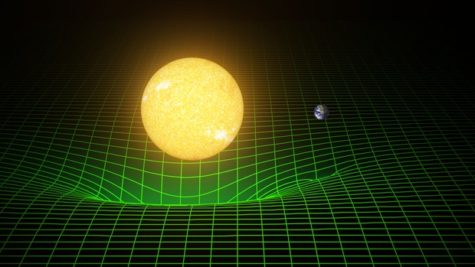
As the name might suggest, the core idea of QFT is that of intangible, extra dimensional “fields” that underlie our world. A field is a property of space containing points, such that each point on that space has some value. This can be best represented by having each point of the space in question extend out into a higher dimension, with the extension proportional to its value. The best way to understand how these fields work is to imagine them extending from two dimensions out to three, rather than three to four. A classic example of this is the diagram of Einstein’s interpretation of gravity, shown in the thumbnail. In this diagram, Earth or some massive body is shown sitting atop a two-dimensional plane, creating a depression in this plane. From our three-dimensional perspective, it is clear that the plane is being warped in three dimensions, creating a “valley” and a down-sloped surface that would cause other bodies sitting atop this plane to slide. However, from the two-dimensional viewpoint of a body in this plane, the three-dimensional warping is not visible, but the resulting sliding is. Thus, it would experience an attractive force towards the mass creating a depression. This is essentially what gravity is to us, but one dimension higher. Extending this up a dimension, we can see how gravity works based on quantum fields. Massive objects create a four-dimensional warping of our three-dimensional space, just as the body in the picture caused a three-dimensional warping of a two-dimensional space. We, as three-dimensional creatures, cannot see this four-dimensional warping, but we do feel its effects– we “slide” down these warped surfaces towards massive objects, pushed forward by a force we call gravity.

However, what makes quantum field theory useful is the fact that this understanding of forces as extra dimensional warping is applicable not only to gravity, but to nearly anything. As it turns out, there are multiple quantum fields with different traits superimposed on top of each other, all overlaid over our three-dimensional reality. One field, for example, might pertain to mass and objects with mass. This means that the distortions in this field are caused by, and in turn impact, anything with mass. We would call this the gravitational field. Another field might pertain to things with a charge. In this field, we could view positive electrical charges as upward “bumps” in the field, and negative charges as downward “bumps.” Nearly anything can be abstracted and represented this way. Things like the gravitational and electromagnetic forces are represented as force fields, matter is represented as a matter field, and even space itself is represented as a metric field. The differences between these different types of fields are a bit beyond the scope of this article.

The uses of this model for understanding natural phenomena come into play once you add the notion of fields “wanting” things. In layman’s terms, things are more stable when they have lower energy. This is due to the nature of entropy, which merits its own article. For now, take it as a given that everything “wants” to minimize its energy. As such, each point in space “wants” to have its value be zero for each of the force fields. Thus, the field wants to be flat. This means that particles will have a tendency to “flow downstream” in their corresponding field, like how water seeks out low ground. If these particles are water and the bumps in their fields are hills, they will seek out the lowest ground they can.

Looking at QFT in this way was how I first got a good grasp on why redox reactions and fluorescence happen, and how QFT can actually be applied to chemistry. In a redox reaction, an electron is transferring from one chemical species to another. Consider the transfer of two electrons from a zinc metal to a copper ion, forming copper metal and a zinc ion. The reaction is denoted as Zn0 + Cu+2 → Zn+2 + Cu0. A brief look at these elements’ locations on the periodic table will reveal that Zn has a higher electron energy than does copper – 39eV versus 34eV, in fact. This means that the bump in the electromagnetic field formed by zinc is higher than that of copper, and electrons will take the first opportunity to flow down this gradient from zinc to copper. Only two electrons flow because as the “water level” in the copper atom rises after two electron transfers, the two are level, and the minimum energy configuration has been reached, and thus, the water’s surface is flat between copper and zinc. In doing this, the electrons decrease their energy. This energy then has to go somewhere – and just as water flowing downstream can be harnessed by a water wheel, this is the same reaction used in the most primitive batteries. Fluorescence is an interesting case – it happens when external energy sources force electrons to a higher energy level, and upon returning to their original energy level, they release energy in the form of light. It is analogous to scooping a bucket of water and dropping it – energy is used to raise the water higher than it ordinarily wants to be, and when it returns to its normal state that energy is released as movement and sound.

However, chemistry is not the only application for this model. In physics, this can be applied to explain gravity, magnetism and electricity. Gravity is the creation of valleys in the gravitational field, as explained earlier. Gravity is an odd field– it wants to be as uneven as possible– but besides that, its mechanics are rather straightforward. Magnetism is a bit more interesting. Magnets create a downward dip at their negative end and an upward bump at the positive, so when the negative side of a magnet encounters the positive side of another, these dips can cancel each other out. Since the field wants to be flat, this creates an attractive force between the two magnets, pulling them to a position where the opposite disturbances will be as closely aligned as possible and canceling them as much as possible in order to make the field flat. Similarly, crossing two positive or two negative disturbances will make them compound, forcing the field into a higher state of distortion. The field does not want this, resulting in a repulsive force to prevent distortion from occurring. Electricity is the flow of electrons down a gradient in potential, AKA disturbance in the electromagnetic field. Thus, like my aforementioned reference to fluorescence, it is analogous to pouring water down a hill. The energy of an electrical current is calculated by voltage (or the difference in potential– AKA the difference in height between the top and bottom of the hill), and amperage (the number of electrons passing per second– AKA how much water you pour). The higher the hill and the more water you pour, the more energy you will release, and the more energy water will generate as it falls down the hill.

I believe this article has already gone on far too long, so I will conclude with that. Hopefully I have given you an interesting and useful tool to understand the world differently, and I hope you have some fun with it.